오늘은 탐색에 대해서 정리해보려고 한다
탐색문제는 항상 코테에서 자주 출제되는 문제이고,
모든 문제의 기본이 되는 알고리즘이니
잘 익혀두어야 한다.

탐색은 주어진 데이터에서 원하는 데이터를 찾아내는 알고리즘이다.
여기서 주어진 데이터는, 정렬 혹은 비정렬된 데이터로 볼 수 있고,
이에 따라 적합한 탐색 알고리즘을 선택하면 된다.
깊이 우선 탐색
깊이 우선 탐색은 그래프의
시작 노드 -> 탐색할 한쪽 분기 를 정하여
최대 깊이까지 탐색 후,
다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘 이다.
말로는 이해하기 어려워서
그림으로 설명하고자 한다.
그래프는 인접리스트로 표현하고,
한번 방문한 노드를 다시 방문하면 안되므로 노드 방문 여부를 체크할 visited[] 리스트를 사용할 것이다.
스택 삽입은 append, 꺼내는 작업은 pop을 사용하면 된다.

먼저, DFS를 시작할 노드를 정하고,
사용할 자료구조를 초기화 해야한다. (인접리스트 구현, 방문리스트 구현, 시작노드를 스택에 삽입)
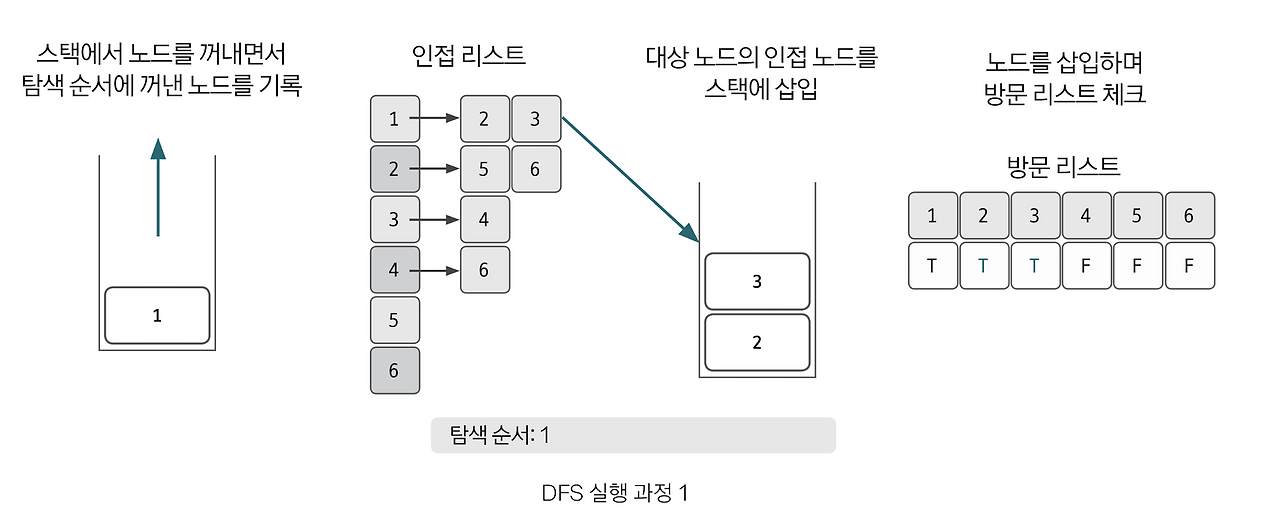
두번째로, 스택에서 노드를 꺼내고
꺼낸 노드의 인접노드를 스택에 넣는다.
그리고 방문리스트를 체크한다.

3번째로는, 앞선 과정을 스택에 값이 없을때까지 반복한다.
이미 방문한 노드는 거치지 않도록 해야한다
여기서 중요한것은,
DFS의 탐색방식은 후입선출 특징을 가지므로 스택을 사용하여 설명을 할 수 있는 것이고,
깊이 우선 탐색은 실제로 재귀함수를 사용한다는 것이다.
깊이 우선 탐색을 응용하여 풀 수 있는 문제는
단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬 등이 있다.
시간 복잡도는 O(V+E)를 갖고 있다.
(V: 노드 수, E: 에지 수)
너비 우선 탐색
너비 우선 탐색은, 시작 노드에서 출발해서
시작노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
가까운 노드를 방문하면서 탐색하기 때문에
목표 노드에 도착하는 경로가 여러개일때,
최단 경로를 구할 수 있다.
너비 우선 탐색도 3가지 과정으로 설명할 수 있다.

먼저, BFS를 시작할 노드를 정한 후 사용할 자료구조를 초기화 해야한다.

두번째는 큐에서 노드를 꺼내면서 인접노드를 큐에 삽입한다.
방문리스트를 체크하면서 이미 방문한 노드는 큐에 삽입하지 않는다.
큐에서 꺼낸 노드는 방문 리스트에 기록한다.

3번째로는, 앞선 과정을 큐가 빌때까지 반복하면 된다.
DFS와는 다르게 선입선출방식을 사용하고,
큐 방식을 사용하여 구현이 가능하다.
시간복잡도는 O(V+E) 이다.
(V: 노드 수, E: 에지 수)
이진 탐색
이진 탐색은 데이터가 정렬되어 있는 상태에서 원하는 값을 찾아내는 알고리즘 이다.
대상 데이터의 중앙값과 찾고자 하는 값을 비교해서 데이터의 크기를 절반씩 줄이면서 대상을 찾는 방법이다.
이진 탐색은 정렬 데이터에서 원하는 데이터를 탐색할 때 사용하는 가장 일반적인 알고리즘 이다.
구현과 원리가 간단해서 많은 코테문제에서 부분문제로 요구하는 것이 많다.
이진 탐색은 오름차순으로 정렬된 데이터에서 4가지 과정을 반복한다.
(만약 내림차순이라면, 조건을 반대로 해서 과정을 반복하면 된다)
이진 탐색 과정
1. 현재 데이터셋의 중앙값을 선택한다.
2. 중앙값 > 타겟 데이터 일때 중앙값 기준으로 왼쪽 데이터셋을 선택한다.
3. 중앙값 < 타겟 데이터일 때 중앙값 기준으로 오른쪽 데이터셋을 선택한다.
4. 과정 1~3을 반복하다가 중앙값==타겟 데이터 인 경우 탐색을 종료한다.

이렇게 이진 탐색을 사용하면 N개의 데이터에서 logN 번의 연산으로 원하는 데이터의 위치를 찾을 수 있다.
16개의 데이터라면 4번의 연산으로 원하는 데이터의 위치를 찾을 수 있다.
(정렬된 데이터를 대상으로 한다는 것을 잊지말자!)
시간복잡도는 O(logN)이다!
'알고리즘 > 개념' 카테고리의 다른 글
| 정렬 - 버블정렬, 선택정렬, 삽입정렬, 퀵정렬, 병합정렬, 기수정렬, 계수정렬 (0) | 2025.03.31 |
|---|---|
| 자료구조 - 스택, 큐, 우선순위 큐 (2) (0) | 2025.03.04 |
| 자료구조 - 배열과 리스트, 구간 합 (1) (0) | 2025.02.08 |
| 코딩 테스트를 준비하기 위한 기초 개념 (시간복잡도, 디버깅) - 디버깅 (0) | 2024.12.31 |
| 코딩 테스트를 준비하기 위한 기초 개념 (시간복잡도, 디버깅) - 시간복잡도 (0) | 2024.12.31 |